유성 기어는 동력 전달 메커니즘으로서 기어 감속기, 크레인, 유성 기어 감속기 등 다양한 엔지니어링 분야에서 널리 사용됩니다. 특히 유성 기어 감속기는 고정축 기어 트레인의 동력 전달 메커니즘을 대체할 수 있는 경우가 많습니다. 기어 변속 과정은 선접촉 방식이기 때문에 장시간 맞물림 시 기어 고장이 발생할 수 있으며, 따라서 유성 기어의 강도를 시뮬레이션하는 것이 중요합니다. Li Hongli 등은 자동 맞물림 방법을 사용하여 유성 기어를 맞물리고 토크와 최대 응력 간의 선형 관계를 확인했습니다. Wang Yanjun 등도 자동 생성 방법을 통해 유성 기어를 맞물리고 정적 및 모달 시뮬레이션을 수행했습니다. 본 논문에서는 주로 사면체 및 육면체 요소를 사용하여 맞물림을 생성하고, 최종 결과를 분석하여 강도 조건이 충족되는지 확인합니다.

1. 모델 구축 및 결과 분석

유성 기어의 3차원 모델링

유성 기어이 기어는 주로 링 기어, 선 기어 및 유성 기어로 구성됩니다. 본 논문에서 선택한 주요 매개변수는 다음과 같습니다. 내륜 기어 톱니 수는 66개, 선 기어 톱니 수는 36개, 유성 기어 톱니 수는 15개, 내륜 기어 톱니의 외경은 150mm, 모듈러스는 2mm, 압력각은 20°, 톱니폭은 20mm, 애더넘 높이 계수는 1, 백래시 계수는 0.25이며, 유성 기어는 3개입니다.

유성기어의 정적 시뮬레이션 분석

재료 속성 정의: UG 소프트웨어에서 작성된 3차원 유성 기어 시스템을 ANSYS로 불러온 후, 아래 표 1과 같이 재료 매개변수를 설정합니다.

메싱: 유한 요소 메쉬는 사면체와 육면체로 나뉘며, 요소의 기본 크기는 5mm입니다.유성 기어선 기어와 이너 기어 링은 접촉 및 맞물림 관계에 있으며, 접촉 및 맞물림 부분의 메쉬는 2mm 크기로 조밀하게 설정되었습니다. 먼저 그림 1과 같이 사면체 격자를 사용하여 총 105,906개의 요소와 177,893개의 노드를 생성했습니다. 그 다음 그림 2와 같이 육면체 격자를 사용하여 총 26,957개의 셀과 140,560개의 노드를 생성했습니다.

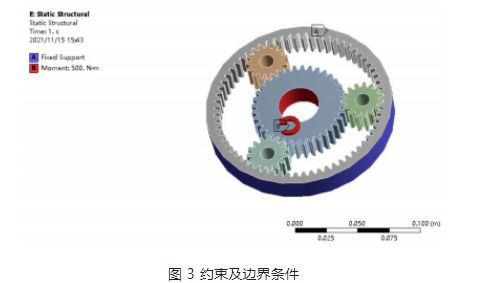
하중 적용 및 경계 조건: 감속기 내 유성 기어의 작동 특성에 따라, 태양 기어는 구동 기어이고, 유성 기어는 피구동 기어이며, 최종 출력은 유성 캐리어를 통해 이루어집니다. ANSYS에서 내부 기어링을 고정하고 그림 3과 같이 태양 기어에 500N·m의 토크를 적용합니다.

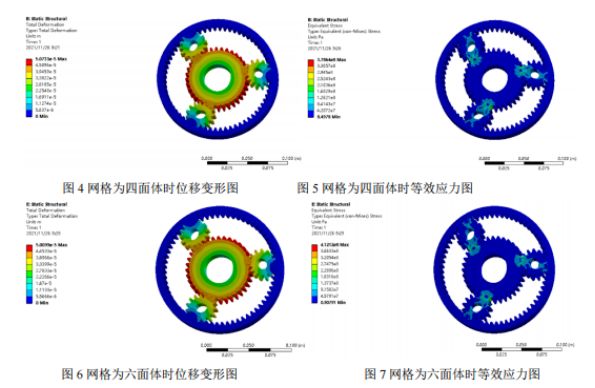
후처리 및 결과 분석: 두 가지 격자 분할을 통해 얻은 정적 해석의 변위 분포도와 등가 응력 분포도를 아래와 같이 제시하고 비교 분석을 수행하였다. 두 격자의 변위 분포도에서 최대 변위는 태양 기어와 유성 기어가 맞물리지 않는 위치에서 발생하고, 최대 응력은 기어 맞물림의 뿌리 부분에서 발생하는 것을 확인할 수 있다. 사면체 격자의 최대 응력은 378MPa이고, 육면체 격자의 최대 응력은 412MPa이다. 재료의 항복 한계가 785MPa이고 안전 계수가 1.5이므로 허용 응력은 523MPa이다. 두 결과 모두 최대 응력이 허용 응력보다 작으므로 강도 조건을 만족한다.

2. 결론

유성 기어의 유한 요소 시뮬레이션을 통해 기어 시스템의 변위-변형 분포도와 등가 응력 분포도를 얻었으며, 이를 통해 최대값과 최소값 및 그 분포를 파악했습니다.유성 기어모델을 찾을 수 있습니다. 최대 등가 응력이 발생하는 위치는 기어 톱니가 파손될 가능성이 가장 높은 위치이기도 하므로 설계 또는 제조 시 특별히 주의해야 합니다. 유성 기어 시스템 전체를 분석함으로써 단일 기어 톱니만을 분석하여 발생하는 오류를 극복할 수 있습니다.